DISTRIBUCION BINOMIAL

 

La distribución binominal  es una distribución de probabilidad  discreta que nos dice el porcentaje en que es probable obtener un resultado entre dos posibles al realizar un número n de pruebas.

La probabilidad de cada posibilidad no puede ser más grande que 1 y no puede ser negativa.

En estas pruebas deberemos tener sólo dos resultados posibles, como al lanzar una moneda que salga cara o cruz o en una ruleta francesa que salga rojo o negro.

Cada experimento es independiente de los otros que hagamos y no influye en las probabilidades de los siguientes, en cada uno la probabilidad de que se de uno de los dos resultados será exactamente la misma.

Por ejemplo, si lanzamos un dado la posibilidad de que el resultado sea par (2, 4 ó 6) o impar (1, 3 ó 5) será exactamente la misma si el dado está bien equilibrado, el 50% y por muchas veces que lo lancemos la probabilidad, en cada una de esas veces, seguirá siendo el 50%.

En la distribución binomial tenemos tres variables:

• n es el número de veces que repetimos el experimento.
• p es uno de los dos resultados al que llamaremos éxito.
• q es el otro resultado posible al que llamaremos fracaso.

Como p y q son los dos únicos resultados posibles, entre los dos su porcentaje debe sumar uno por lo que p=1-q.

Para hacer el experimento lo primero que tenemos que hacer es definir p , es decir, en el ejemplo del dado definir si éxito o p es que salga un número par o impar; a partir de ahí, q será la otra posibilidad.

Otro ejemplo: supongamos que vamos con prisa por la calle y queremos tomar un taxi, vamos a calcular la probabilidad de que el próximo taxi que pase esté libre u ocupado. Como hoy está lloviendo es muy probable que esté ocupado. Vamos a asignar a la probabilidad de que esté libre un 15% (es decir, 0,15). Si definimos p o éxito como la probabilidad de que esté libre la de que esté ocupado será q que, al ser 1-p será 1-0,15, es decir 0,85 o, dicho en porcentaje, el 85%

Así, si queremos saber la probabilidad de que un resultado ocurra determinadas veces utilizaremos estos porcentajes.

Por ejemplo, si observamos que pasan diez taxis y queremos saber la probabilidad de que tres de ellos estén libres la fórmula sería:

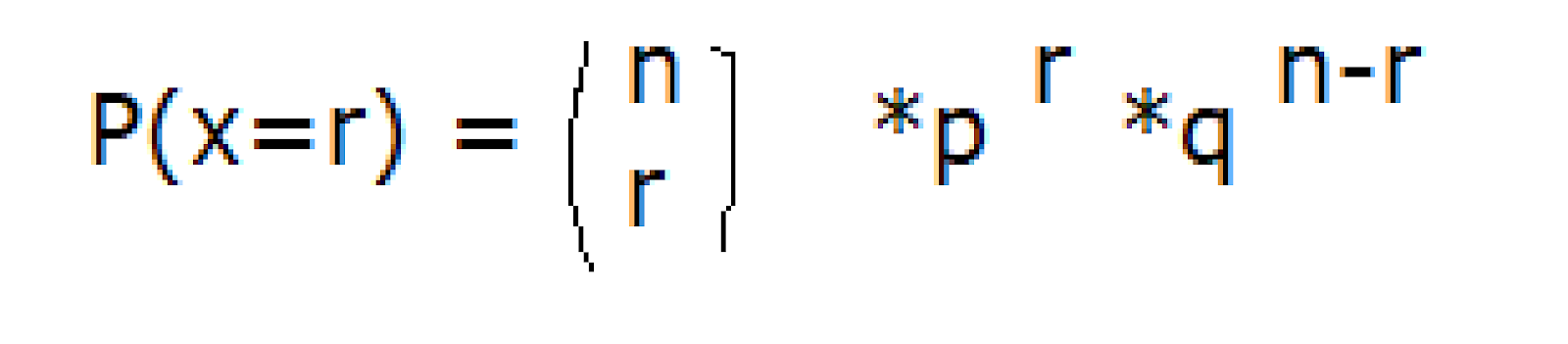
Donde P es la probabilidad de que tres taxis de los diez estén libres, r las veces que queremos calcular que estén libres, en este caso tres, p el porcentaje de éxito, en este caso 0,15, elevado a r, que hemos visto antes, por q (el porcentaje de fracaso que, en este caso es 0,85) elevado a n menos r; n sobre r se calcula utilizando números factoriales.

Condiciones para una distribución binomial

Una distribución se denomina binomial cuando se cumplen las condiciones siguientes:

• El experimento aleatorio de base se repite n veces, y todos los resultados obtenidos son mutuamente independientes.
• En cada prueba se tiene una misma probabilidad de éxito (suceso A), expresada por p. Asimismo, existe en cada prueba una misma probabilidad de fracaso (suceso ), que es igual a q = 1 - p.
• El objetivo de la distribución binomial es conocer la probabilidad de que se produzca un cierto número de éxitos. La variable aleatoria X, que indica el número de veces que aparece el suceso A (éxito), es discreta, y su recorrido es el conjunto {0, 1, 2, 3, ..., n}.

La distribución binomial se expresa como B (n, p), siendo n el número de veces que se repite el experimento y p la probabilidad de que se produzca un éxito.

Ejemplo de experimento aleatorio descrito por una distribución binomial: al tirar un dado cuatro veces, ¿cuántas veces saldrá el número 6? Este suceso es el «éxito» del experimento.

Función de probabilidad

La distribución binomial se caracteriza porque su función de probabilidad viene dada por la expresión siguiente:

donde r es el número de éxitos asociado al experimento aleatorio.

En una distribución binomial B (n, p) se verifica que:

• La probabilidad de que aparezca al menos un éxito en las n repeticiones es igual a:
  

• La probabilidad de que se produzca un éxito como máximo en las n repeticiones se determina como:
  

Esperanza, varianza y desviación típica

En una distribución binomial denotada por B (n, p), donde n es el número de repeticiones del experimento y p la probabilidad de que se produzca un cierto suceso (éxito), la esperanza matemática de la variable aleatoria X viene dada por la expresión siguiente:

Análogamente, la varianza de la variable aleatoria X, al ser ésta de tipo discreto, se calcula como:

siendo q la probabilidad de no éxito (fracaso). La desviación típica es, como de costumbre, la raíz cuadrada de la varianza:

Ajuste de una distribución binomial

En ocasiones, el cálculo de la probabilidad de una distribución binomial del tipo B (n, p) resulta muy complicado. Según demostró el matemático francés Abraham de Moivre (1667-1754), la probabilidad de una distribución binomial B (n, p) puede aproximarse por medio de una distribución normal (ver t56) de tipo N (np, ), que resulta particularmente adecuada cuando:

• El valor de n es muy elevado.
• Tanto np y nq son ³ que 5. (Obsérvese que cuanto mayor es n y más se aproxima p a 0,5 tanto mejor es la aproximación realizada).

Para transformar una distribución binomial (de variable discreta) en una normal (de variable continua), es preciso proceder a la siguiente transformación: