METODO DE ASIGNACION

 

El modelo de asignación es un caso especial del modelo de transporte, en el que los recursos se asignan a las actividades en términos de uno a uno, haciendo notar que la matriz correspondiente debe ser cuadrada. Así entonces cada recurso debe asignarse, de modo único a una actividad particular o asignación.

Se tiene un costo Cij asociado con el recurso que es asignado, de modo que el objetivo es determinar en que forma deben realizarse todas las asignaciones para minimizar los costos totales.

El modelo de asignación es un tipo especial de problema de programación lineal en el que los asignados son recursos que se destinan a la realización de tareas. Por ejemplo, los asignados pueden ser empleados a quienes se tiene que dar trabajo. La asignación de personas a trabajos es una aplicación común del problema de asignación. Sin embargo, los asignados no tienen que ser personas. También pueden ser máquinas, vehículos o plantas, o incluso periodos a los que se asignan tareas.

“La mejor persona para el puesto” es una buena descripción del modelo de asignación.

     El objetivo del modelo es determinar la asignación óptima (de costo mínimo) de trabajadores a puestos.

El modelo general de asignación con n trabajadores y n puestos se representa en la tabla siguiente:

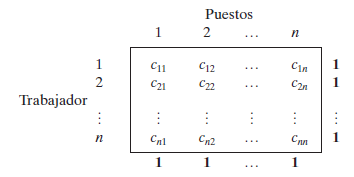
     Para que se ajuste a la definición de un problema de asignación, es necesario que este tipo de aplicaciones se formule de manera tal que se cumplan los siguientes supuestos:

1. El número de asignados es igual al número de tareas. (Este número se denota por n.)
2. A cada asignado se le asigna sólo una tarea.
3. Cada tarea debe realizarla sólo un asignado.
4. Existe un costo cij asociado con el asignado i (i 5 1, 2, . . . , n) que realiza la tarea j ( j 1, 2, . . . , n).
5. El objetivo es determinar cómo deben hacerse las n asignaciones para minimizar los costos totales.

Se puede resolver el modelo de asignación en forma directa como modelo normal de transporte. Sin embargo, el hecho de que todas las ofertas y las demandas son iguales a 1, condujo al desarrollo de un algoritmo sencillo de solución llamado método húngaro.

METODO HUNGARO

EJEMPLO 

Un equipo de 3 mecánicos debe ser asignado para la realización de 3 tareas, donde cada mecánico debe hacer una tarea. Se requiere encontrar la asignación de costo mínimo para lo cual se dispone de los costos asociados a que el mecánico i realice la tarea j.

SOLUCIÓN

PASO 1: En la matriz original de costo, identificar el mínimo de cada renglón y restarlo de todos los elementos del renglón.

PASO 2: En la matriz que resulte del paso 1, identificar el mínimo de cada columna, y restarlo de todos los elementos de la columna.

PASO 3: Identificar la solución óptima como la asignación factible asociada con los elementos cero de la matriz obtenida en el paso 2.

Las celdas con valor cero y color cafés son la solución óptima. En consecuencia el mecánico 1 realiza la tarea 2, el mecánico 2 asuma la tarea 1 y el mecánico 3 la tarea 3. Cada mecánico realiza exactamente una tarea y el costo total de dicha asignación (valor óptimo) es de Q9+Q10+Q8=Q27.