¿QUE ES Y PARA QUE SIRVE EL METODO SOLVER?
El General Problem Solver (GPS), en español Solucionador General de Problemas, es un programa de ordenador creado en 1957 por Herbert Simon, J.C. Shaw, y Allen Newell con el objetivo de construir una máquina capaz de resolver problemas de carácter general. Cualquier problema simbólico formal puede ser resuelto, en principio, por el GPS. Por ejemplo: probar teoremas, resolver problemas geométricos, trabajar con lógica proposicional y jugar al ajedrez. Se basaba en el trabajo teórico previo de Simon y Newell sobre máquinas lógicas.
Solver es una herramienta o complemento de Excel que nos permite realizar cálculos para alcanzar un resultado.
Es decir, que con el Solver podemos encontrar objetivos optimizados para modelos lineales y no lineales.
Específicamente el Solver nos ayuda hacer análisis como por ejemplo determinar el valor máximo o mínimo de una celda, realizando variables o cambios en otras celdas y permitiéndonos encontrar la solución más óptima a un problema
Y es una herramienta que podemos aprovechar mucho en ambientes o escenarios como el logístico o de producción.
Para que tengamos un mejor entendimiento sobre como usar el Solver en Excel, vamos a hacer el siguiente ejercicio y vamos a resolverlo a través de la aplicación de la herramienta del Solver Excel.
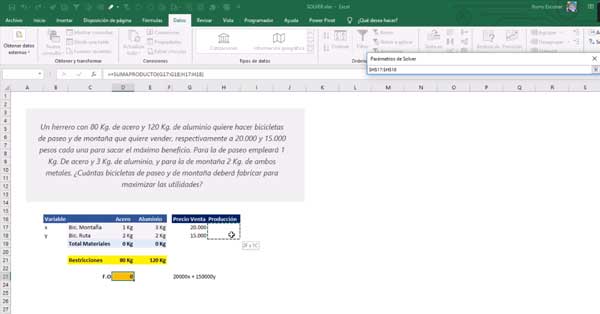
“Un herrero con 80Kg de acero y 120Kg de aluminio, quiere hacer bicicletas de paseo y de montaña para vender, respectivamente a 20.000 y 15.000 pesos cada una para sacar el máximo beneficio. Para la de paseo, empleara 1 kg de acero y 3kg de aluminio, y para la de montaña 2kg de ambos materiales. ¿Cuántas bicicletas de paseo y de montaña deberá fabricar para maximizar las utilidades?
Entonces, tengamos en cuenta que un modelo de programación lineal siempre se plantea bajo dos supuestos. Uno es, establecer la función objetivo y dos tener en cuenta las restricciones del problema.
Lo primero que debemos hacer es organizar la información del problema de forma ordenada y formulada, para prepararla al momento en que ejecutemos el Solver Excel.
Como vemos en la anterior imagen, tenemos dos variables X y Y, una es bicicleta de montaña y otra es bicicleta de rutas y tenemos los datos o materiales ordenados y que corresponden a cada una y también tenemos el precio de venta.
¿PORQUE NECESITAMOS UTILIZAR EL SOLVER PARA RESPONDER ESTE EJERCICIO?
Cualquiera podría decir que si vendemos la bicicleta de montaña por mayor valor, todo el material que tenemos, lo vamos a utilizar en producir bicicletas de montaña. Pero lo que se busca, es una función objetiva que maximice el beneficio.
👉¿Por qué?👈
Porque si para la bicicleta de montaña necesito 1kg de acero y 3kg de aluminio y nos gastamos los 80kg de acero en producir bicicletas de montañas,
podemos hacer 80 bicicletas. Pero resulta que de aluminio por cada bicicleta vamos a utilizar 3kg del material y tenemos 120kg, con lo cual nos daría solo para producir solo 40 bicicletas.
Es decir, que nos estaría sobrando un material si decidiéramos producir solo en acero o en aluminio. Entonces, tendríamos un material que podríamos utilizar en la producción de la bicicletas de ruta.
PLANTEAMIENTO DEL EJERICIO Y LA FUNCION
La sección de Producción, son las variables que no sabemos y que queremos hallar, para poder generar la producción del producto. Ahora necesitamos saber el total de materiales. Y ¿a qué es igual el total de materiales? pues básicamente a la multiplicación de lo que emplee de acero versus lo que se produzca, para esto utilizamos la función +SUMAPRODUCTOS

Y abajo en amarillo tenemos las restricciones, que nos la da el problema, la cual dice que el herrero tiene 80kg de acero y tiene 120kg de aluminio, es decir que nosotros no podemos superar esa cantidad de material, podemos utilizar menos pero no más.
Por último, lo más importante es plantear la Función Objetivo (F.O). Y ¿Cuál es la función objetivo de este ejercicio? Si la hacemos matemáticamente, la función de ejercicio seria (20.000 X + 15.000 Y) ósea el precio de venta por lo que produzca bicicletas de montaña y por lo que produzca bicicletas de ruta
Queremos encontrar el máximo valor que eso nos pueda generar, es decir las variables X y Y que nos produzca los mayores beneficios, teniendo en cuenta las restricciones.
La Función Objetivo es la matriz de precio venta por la matriz de producción, que es nuestra variable independiente e incognitica que tenemos en el momento.

ACTIVAR EL SOLVER Y UTILIZARLO PARA RESOLVER EL EJERCICIO
Vamos a resolver el ejercicio con el Solver. Lo primero que debemos hacer es activar el Solver, recuerde que el Solver es un complemento y debemos activarlo en el Excel.
Para activar el Solver debemos irnos a Archivo – Opciones – Complementos – Complementos de Excel – Solver. Marcamos el completo y activamos. Ahora nos vamos a la ficha datos y le damos clic en Solver

Establecemos el objetivo, recordemos que es la Función Objetivo que en el archivo del ejercicio la hemos denominado F.O; entonces seleccionamos esa celda.
¿MAXIMIZAR O MINIMIZAR LOS OBJETIVOS?
La función objetivo puede ser para maximizar, para minimizar o para llegar a un valor X. Normalmente las funciones objetivo para maximizar se pueden aplicar a opciones como ingresos de utilidades, que generan valor y de minimizar son aplicables a costos de operaciones.
Para el ejercicio dejamos marcado Max y pasamos a la siguiente opción cambiando las celdas de variables. Donde las celdas que nos van a hacer mover todo el modelo y que nos van a arrojar un valor en la función objetivo son las variables incógnitas, ósea lo que debemos producir de X y Y, es decir de bicicletas de montaña y bicicletas de ruta.
En síntesis, lo que vamos a poner son las variables que desconocemos y que nos van a ayudar a calcular el Solver para poder conocer cuál es el máximo ingreso que podemos obtener del ejercicio.
Ahora vamos a agregar las restricciones, en las cuales tenemos que en acero hay 80 kg y en aluminio 120 kg


Ahora ya tenemos todo el modelo listo, con nuestro objetivo, que es la celda Función Objetivo (F.O), las celdas que debe cambiar que serían prácticamente las variables que no conocemos.


Comentarios
Publicar un comentario